When Does A System Of Equations Have No Solution
When does a system of equations have no solution. It is impossible for the equation to be true no matter what value we assign to the variable. So lets think about how we can go about doing this. Write the systems of inequalities whose shaded region is the solution set.
Infinite solutions would mean that any value for the variable would make the equation true. Which impossible 0 cannot equal -3. Left beginarraycccc -3-12 1 0 frac-53 frac103 frac83 00 0 textany non-zero endarray right.
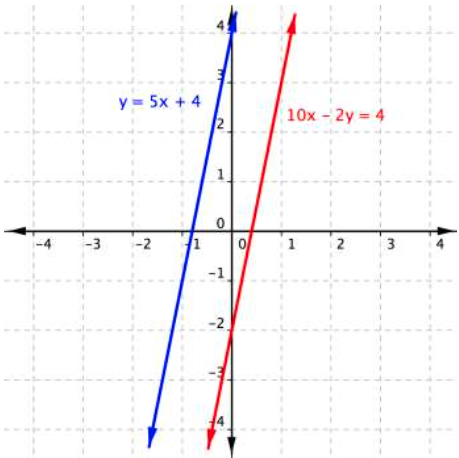
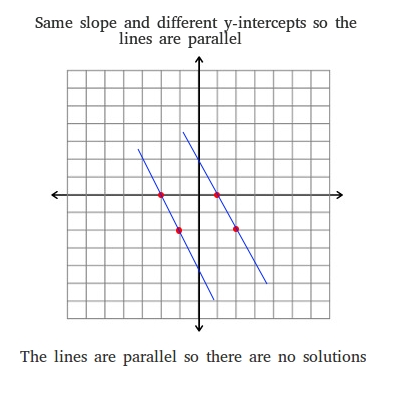
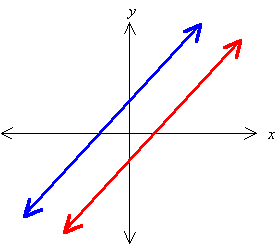
Ask Question Asked 4 years 11 months ago. When graphed the lines will have the same steepness with different beginaligny-endalignintercepts. 2x - 3y z 0 x ay 2z 0 x y - z 0 How do you determine from equations alone whether with a or not the system represents infinite solutions.
Let us consider the pair of linear equations in two variables x and y. The solution to these variables must satisfy. Systems of equations are classified as independent with one solution dependent with an infinite number of solutions or inconsistent with no solution.
From an algebra standpoint this means b2 4ac. In general a system with more equations than unknowns has no solution. One or infinitely many solutions are called consistent.
There is no solution when the matrix is textbfinconsistent. Here a 1 b 1 c 1 a 2 b 2 c 2 are all real numbers. A quadratic equation has no solution when the discriminant is negative.
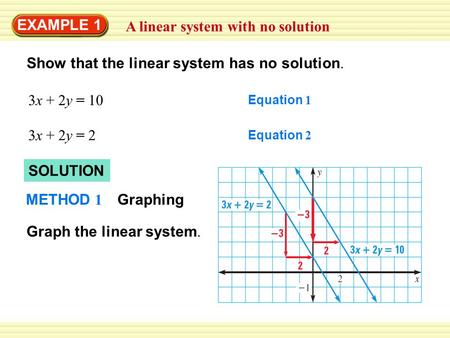
Therefore this system of linear equations has no solution. When does a system of equations have infinite unique and no solutions.
When does such a system have a unique solution.
An inconsistent system of equations is a system of equations that has no solution. In this case the solution set is empty. A system has no solution if the equations are inconsistent they are contradictory. Visually this means the graph of the quadratic a parabola will never touch the x axis. A 2 x b 2 y c 2 0. B If d 1 d 2 d 3 0 d_1d_2d_30 d 1 d 2 d 3 0 then system of linear equations is known as Homogeneous linear equations which always possess at least one solution ie. For example there do not exist numbers x and y making the following two equations true simultaneously. A 1 x b 1 y c 1 0. 2x - 3y z 0 x ay 2z 0 x y - z 0 How do you determine from equations alone whether with a or not the system represents infinite solutions.
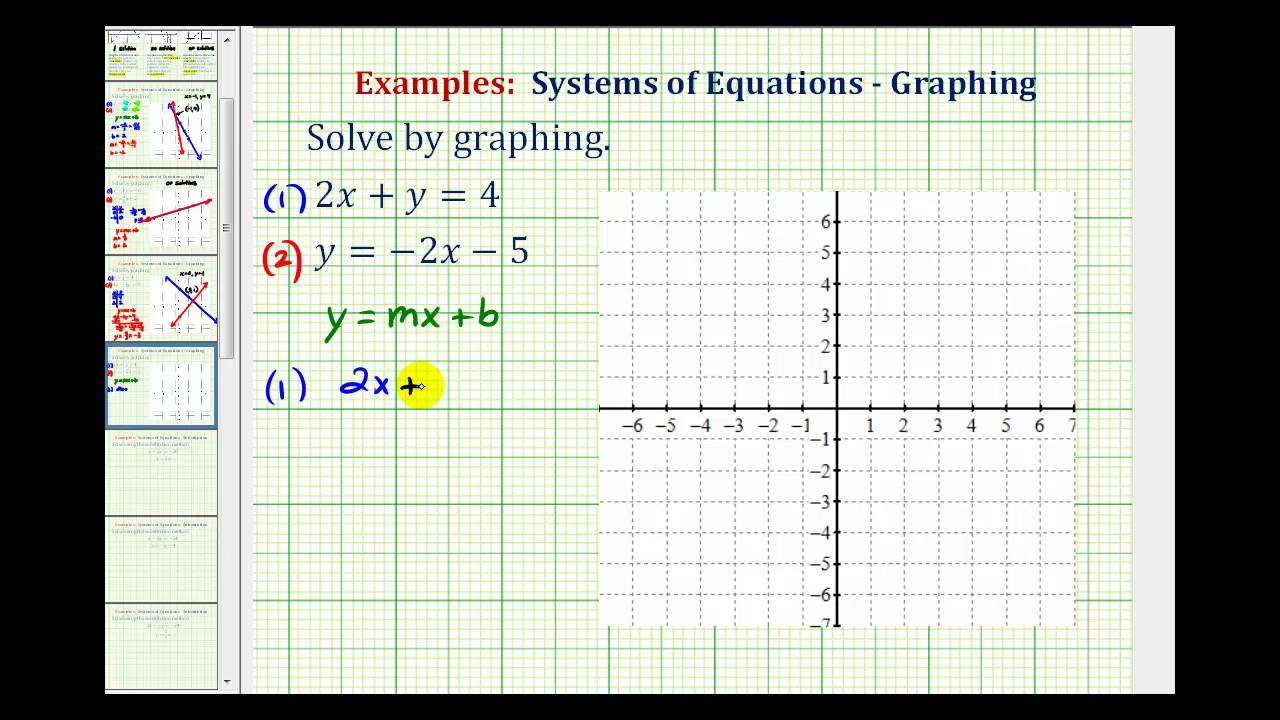
In a system of n linear equations in n unknowns AX B if the determinant of the coefficient matrix A is zero no solution can exist unless all the determinants which appear in the numerators in Cramers Rule are also zero. This article reviews all three cases. Which impossible 0 cannot equal -3. One method of solving a system of linear equations in two variables is by graphing. Determine whether the system has no solutions or infinite solutions. I have been searching the internet and I cannot find a straightforward answer of. A system of linear equations need not have a solution.





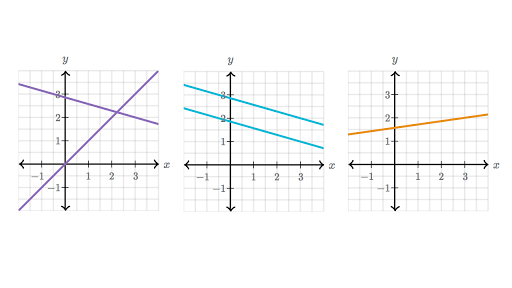





























Post a Comment for "When Does A System Of Equations Have No Solution"